Abstract
Background: Aiming point analysis systems are commonly used in sports shooting but face four main challenges: they do not account for intra-session variations, they overlook inter-individual shooter preferences, they ignore compensation mechanisms of technical features, and they do not respect the real shot location at the target. The aim of this study is to investigate the effects of compensation-sensitive, shot styles on performance while accounting for the mentioned challenges. Methods: To address the first two challenges, we developed and validated an automated movement phase detection algorithm. When compared to three independent expert ratings, the algorithm demonstrated a high correlation (r = .811). Building on this algorithm and addressing challenge 3 and 4, this study applied cluster-analysis and ANOVA to determine the performance relevance of compensation-sensitive shot styles using datasets from a single athlete and 26 advanced to elite level athletes. Results: Significant performance differences in shot styles for both datasets, with each shot style distinctively differing from the others were found. Conclusions: Shot styles which allow for compensation and intra-individual movement phase differences exhibit performance variations. Coaches and athletes should emphasize holistic training, focusing on combinations of features that allow for compensation.
Keywords
shooting, aiming, performance, hold, stability, compensation, feature reduction, machine learning
Introduction
Olympic air rifle shooting places extreme precision demands on athletes. The limit to qualify for the finals at the 2022 World Championships in Cairo was over 630 points and, even when extended to junior finals, only 3 of 8 qualified athletes scored less than 630 points. This corresponds to an average shot result of 10.5 points for the 60 shots fired in qualification and equals to an average radial deviation of 1.25 mm to the target’s center in 10 m distance.
To shed further light on the mechanisms of such precision performance, a domain-specific breakdown of potential aspects seems necessary. Environmental conditions, material-specific and athlete-specific aspects have previously been identified as fundamental domains in several systematic reviews on shooting performance (Chung et al., 2006; Spancken et al., 2021; Sundaram et al., 2024). As Olympic air rifle shooting is an indoor discipline that is strictly regulated, environmental conditions, e.g., with respect to lighting conditions and dimensions of shooting ranges, can largely be neglected. According to experts, material properties would only account for a loss of 0.04 points per shot (Bühlmann & Reinkemeier, 2022). Therefore, with the best material currently available, a score of 651.6 out of the possible maximum of 654 should be reachable provided an errorless technique. This, however, seems in stark contrast to the 630 points mentioned above and constitutes the fact that the greatest performance improvement potential lies in improving the shooter’s motor control.
Taking a purely biomechanical perspective while neglecting further material and ballistic aspects, the rifle can be treated as a rigid body whose three translational and three rotational degrees of freedom are only constrained by the shooter’s biomechanics (International Shooting Sport Federation, 2022). These six degrees of freedom of the rifle influence directly the location of the aiming point, which is the intersection point of the rifle’s forward vector with the target in 10 m distance. The trajectories of this aiming point over time are called aiming point fluctuations. To guarantee a performance of 10.5 points, the aiming point fluctuations need to constantly remain within the 1.25 mm radial deviation from target centre mentioned above, when assuming no mean systematic bias away from the target centre. For this, maximum translational movements of 1.25 mm are tolerable, while rotational movements must not exceed .007°, unless coupled translational and rotational movements compensate the movement of the aiming point. Interestingly, the six degrees of freedom of the rifle’s movements controlled by the shooter are finally reduced to only two performance relevant degrees of freedom, namely the vertical and horizontal aiming point fluctuation on the target plane.
As the aiming point fluctuation of a high-performance shooter are hardly visible to the naked eye, coaches and athletes rely on aiming point analysis systems (Noptel, n.d.; SCATT, n.d.; TRACE Electronic Shooting Systems, n.d.). These aiming point analysis systems comprise of a sensor mounted to the rifle which tracks the target via camera or estimates the rifle movement via inertial measurement units. Data are sent from the sensor to a software system where features of the aiming point fluctuation are calculated that are intended to provide information about skill-related features of the aiming point fluctuation.
In practice literature (Bühlmann & Reinkemeier, 2022), the aiming point fluctuations are often structured in four functionally different phases: an approach phase, an aim-and-hold phase, a trigger phase, and a recoil phase. The approach phase begins with the aiming point entering the value range of the target and ends when entering the individual holding and aiming area, which ideally lies at the center of the target. There, the athlete aims and holds for an individually different duration until the pressure point on the trigger is overcome and the shot is released. The reaction of the rifle to the recoil of the bullet causes a movement of the aiming point on the target that is accelerated to a certain direction followed by a fallback towards the holding area. While the general structure of the aiming point fluctuation is identical independent of the athletes’ skill level, structural differences are still present in finer details of the aiming point fluctuation which may call for athlete- and/or skill-level-dependent analysis procedures.
However, the characteristics of the phase segmentation algorithms implemented in current aiming point analysis systems differ from state-of-the-art training literature. In effect, four potentially confounding factors arise when it comes to aiming point analysis systems: First, movement phases are applied to all shots based on a temporal phase division without considering intra-session variations. This can result in technical features of individual shots being evaluated based on functionally inappropriate temporal intervals, leading to variables being calculated for only a fraction of functionally distinguishable shooting phases or even for overlapping phases (Bale & Wilkinson, 2023; Ihalainen et al., 2017; Lang & Zhou, 2021; Mon-López et al., 2022; Zanevskyy et al., 2009). Second, inter-individual preferences are not considered, such as the distinction between reaction shooters with shorter aiming times, holding shooters with longer aiming times, or optimizers with slow approaching phases (Liu & Mao, 2000; Yli-Jaskari & Heinula, 2009). In our view, a more appropriate approach would be to calculate features based on the functional structure of the movement (Hossner et al., 2020), rather than solely on the temporal component. Third, compensation mechanisms of different technical features are ignored (Arutyunyan et al., 1969; Baca & Kornfeind, 2012; Yli-Jaskari & Heinula, 2009; Zatsiorski & Aktov, 1990). For example, a higher mean aiming error can be compensated by leveraging a late target-centre-directed aiming point movement and controlling the trigger force to release the shot at the optimal point in time. In this specific case, features of the aim-and-hold and trigger phase would indicate a bad technique, while the shot result would still be high. Fourth, evidence from training practice suggests that virtual performance measurements rarely coincide with real shot outcomes. This can be attributed to varying material properties of the rifle and ammunition, hardware limitations of current aiming point sensors and missing or inaccurate models of ballistic processes in the software implementations of current aiming point analysis systems. On the other hand, electronic target systems determine real shooting performance with less than 0.01 mm accuracy (International Shooting Sport Federation, 2013; SIUS AG, 2024). To date, there are no published validation studies comparing the accuracy of the aiming point analysis systems to electronic target systems.
This study aims to evaluate the accuracy of a phase segmentation algorithm against expert ratings, focusing on functional structuring while accounting for variations in durations of movement phases both inter- and intra-individually. As a second goal, we seek to identify compensation-sensitive shot styles by identifying performance-relevant technical features at both the intra-individual level, across multiple shots and sessions for a single athlete, and the inter-individual level, across multiple shots and sessions for multiple athletes. The third and final goal is to determine performance differences of inter- and intra-individual shot styles with regards to real performance.
Methods
Study design and participants
This study applies an observational research design to elucidate the influence of shot styles on real shooting performance. To consider intra-individual and inter-individual aspects, we utilized two datasets. Firstly, an individual athlete (SING) who independently completed multiple training sessions with varying numbers of shots over a prolonged period from November 2019 until March 2022. Secondly, a more heterogeneous dataset (HE) consisting of standardized measurement sessions conducted as part of the accompanying diagnostics during training camps for the Swiss elite and junior national teams from July 2021 to July 2023. All participants used their personal air rifles and shooting equipment. The measurement sessions were conducted at the 10 meters shooting range of the national shooting federation’s shooting venue. Participants were required to shoot in the standing position and all shots were live-fired according to the ISSF Regulations (International Shooting Sport Federation, 2022). Shooting performance was measured using real shot coordinates (SIUS AG, 2024). For a detailed overview on the two datasets consider Table 2.
Procedure
Data recording for HE and SING differed regarding the measurement software and the immediate feedback after each shot. Aiming point fluctuation for HE and SING was recorded using two different custom-written software that combined real performance data (SIUS AG, 2024), virtual aiming point fluctuation provided by the SCATT System (SCATT, n.d.) and other sensory data that are not relevant for the present study. The shooters of HE did not receive any feedback on their movement execution during the shooting session, only the shot position was displayed on a monitor next to the shooter after each shot. The athlete of SING did receive immediate visual feedback (1 s delayed after shot execution) on movement execution after each shot during the shooting sessions regarding aiming point fluctuation and trigger pressure over time because of a specific training regime in preparation of international competitions. Because we expect the augmented visual feedback of shot execution to affect the behaviour of the shooter we treated the two datasets separate.
Since not all athletes in HE performed an equal number of training sessions due to different training and competition schedules, we set a minimum number of 50 shots to be available per athlete across all sessions. This guaranteed an even selection of shots for each athlete, preventing bias towards those who had more training shots during the period of this study.
Data processing of phase segmentation and validation
For the validation of the phase segmentation algorithm, the following three steps were conducted with a custom script written in MATLAB R2023a (The Mathworks Inc., 2023): In the first step, the moment of shot release is identified by setting a time window of ± 0.03 seconds around the estimated moment of the shot. Within this window, the algorithm calculates a “shake” metric from the radial distance, indicating movements that could correspond to a shot. The detection mechanism searches for the first occurrence where this shake exceeds a predefined threshold, indicating the occurrence of a shot. If no shot is detected within the initial parameters, the algorithm iteratively adjusts the threshold until a shot is found.
In the second step, the aiming point trajectories are corrected from relative positions to exact locations (SIUS AG, 2024). Each data point is adjusted so that the virtual shot position determined by the shot detection algorithm precisely matches the coordinates of the real shot position. After this offset correction, the trajectory of the aiming point matches the real trajectory, without considering external ballistics.
The third step employs a refined movement phase segmentation algorithm for accurate examination of the temporal characteristics of specific shot phases. This step includes precise segmentation of the aiming point trajectory into well-defined phases, including the approach phase and the hold-and-aim phase. Special focus was put on the approach phase, where significant change points are identified through a combination of data points, such as slope and mean of the trajectory (Killick et al., 2012; Lavielle, 2005). These are further analysed using advanced clustering methods, such as k-means clustering (Arthur & Vassilvitskii, 2007; Lloyd, 1982), to detect and group homogeneous behavior patterns within the data. A silhouette analysis (Kaufmann & Rousseeuw, 1990) is then conducted to rate the clusters according to their relevance for the approach phase and to set the characteristic segmentation of the two phases approach and hold-and-aiming-phase. To ensure reliability of the algorithm, three experts of the National Shooting Federation rated 720 shots performed by 12 athletes from HE using a custom graphical MATLAB software (The Mathworks Inc., 2023). A salient feature of this software is a slider mechanism, enabling experts to color-code the distinct phases of the shot trajectory into approach phase and hold-and-aiming phase. The efficacy and accuracy of the approach detection algorithm was analysed by employing Pearson correlation coefficients to discern the degree of concordance between the algorithm-derived results and the evaluations by experts. Further, inter-expert correlation was calculated.
Data processing for compensation sensitive shot styles
For the identification of inter- and intraindividual shot styles three steps had to be performed. In the first step, feature computation for every movement phase was carried out. For a comprehensive breakdown of all features, we refer the reader to Table 1 . While our analysis did incorporate traditional features as per the recommendations from prior research (Ball et al., 2003; Ihalainen et al., 2016, 2017; Lang & Zhou, 2021; Mon-López et al., 2022), we further introduced new features to address ceiling effects in the commonly used stability of hold values 10a0 of SCATT (SCATT, n.d.). Moreover, the application of the approach detection algorithm allows for the identification of a movement phase that had not been previously analysed for potentially relevant features. Previously, a purely temporal separation between the movement phases in rifle shooting resulted in a blend of the two phases approach and hold-and-aiming phase. With the implementation of the approach detection algorithm, this structural separation becomes more precise, enabling the isolation and distinct examination of the movement phases. This enhanced distinction prevents unintended merging of the two phases, allowing for an unconfounded analysis of the shooter's aiming procedure. Our method significantly improves upon previous approaches by introducing a Timing feature, which differs from the time-focused Tire characteristic described by Ihalainen, Kuitunen, et al. (2016) through its use of a spatial and directional perspective. Unlike Tire, which identifies the moment of minimal radial distance to the target's center, prioritizing closer distances at shot release as optimal, our method builds on this concept but also incorporates insights from Goodman et al. (2009). Our key advancement is the identification of the last direction change before shot release. Unlike Goodman et al. (2009), who analyze angle values between the current movement trajectory and the orientation towards the target center at each moment before release, our focus narrows to the angle after the final significant directional shift. This angle, measured between the final aiming point movement direction and the line to the target center, ranges from 0 degrees (direct movement towards the target) to 180 degrees (movement away from the target).
In the second step faulty shots and those with feature outliers were excluded. Outliers were detected using the Mahalanobis distance (Mahalanobis, 1936) and considering the hierarchical dataset structure. Shots scoring below 9.0 were discarded because we were mainly interested in the differences within the high scoring shots. Typically, high performance level athletes in Olympic air rifle shooting as in this study can easily identify errors in shots below 9.0 by themselves.
The third step applies only for HE and was carried out to ensure that a minimal equal number of shots (n = 50) was drawn for each athlete in order to a) get the most possible shots for HE and b) avoid weighting of athletes in the following steps of data processing. The draw was performed while assuring a minimal difference in mean and standard deviation of each athlete’s population mean in real performance and could be characterized as semi-random.
Feature | Description |
|---|---|
siusX | horizontal deviation of real shot location [mm] |
siusY | vertical deviation of real shot location [mm] |
dec | real decimal scoring according to ISSF regulations [rings] |
cont | radial deviation of real shot location [mm] |
minTV | start of approach phase [s before shot release] |
appTV | end of approach phase [s before shot release] |
appMeanVelocity | mean aiming point velocity during approach phase [mm/s] |
appVelocityChange | slope of aiming point velocity changes during approach phase [mm/s^2] |
appStdVelocity | SD of aiming point velocity during approach phase [mm/s] |
appSway | SD of aiming point distance to linear fitted approach vector [mm] |
appAngle | angle of linear fitted approach vector to vertical axis [°] |
appInterPeakTime | mean absolute temporal spacing between peaks along linear fitted approach vector [s] |
appPeakFrequency | number of peaks along linear fitted approach vector per second [Hz] |
aimingError | distance of average aiming point (centre of hold and aiming phase) to target centre [mm] |
aimMeanVelocity | mean velocity during hold and aiming phase [mm/s] |
aimStdVelocity | SD of velocity during hold and aiming phase [mm/s] |
aimInterPeakTime | mean absolute temporal spacing between peaks around average aiming point [s] |
aimPeakFrequency | number of peaks around average aiming point per second [Hz] |
aimPeakAmplitudeTrend | slope of amplitude of peaks around average aiming point over time [mm/s] |
hold10a5 | relative number of aiming points within circle of radius 1.25 mm around average aiming point [%] |
hold10a0 | relative number of aiming points within circle of radius 2.5 mm around average aiming point [%] |
holdEllipseArea | area of rotated ellipse with 2 SD fitted to aiming points of hold and aiming phase [mm^2] |
holdSmallestCircleRadius | radius of smallest circle around aiming points of hold and aiming phase [mm] |
aimingAccuracy10 | relative number of aiming points placed within the circle around the target centre with radius 2.5 mm [%] |
aimingAccuracy105 | relative number of aiming points placed within the circle around the target centre with radius 1.25 mm [%] |
relTimingAimCentre | scaled angle between vector of last trajectory before shot release and average aiming point. 0: trajectory leading away from average aiming point; 100: trajectory leading towards average aiming point [score] |
relTimingTargetCentre | scaled angle between vector of last trajectory before shot release and target centre. 0: trajectory leading away from target centre; 100: trajectory leading towards target centre [score] |
relMeanVelocity | mean aiming point velocity during release phase [mm/s] |
relMeanVelocityChange | slope of aiming point velocity changes during release phase [mm/s^2] |
relPeakFrequency | number of peaks around average aiming point per second [Hz] |
relImpulse | distance between average aiming point and shot location [mm] |
tire | time stamp of minimal radial distance of aiming point fluctuation to target centre within release phase [s before shot release] |
cleanness | mean aiming point velocity of release phase relative to mean velocity of hold and aiming phase [%] |
Statistical analysis
To check for normal distribution, a skewness measure was employed, but given the dataset’s size, normality tests were not. Features showcasing an absolute skewness beyond 0.5 (Hatem et al., 2022) underwent Box-Cox transformation (Box & Cox, 1964; Daimon, 2011). Those still not meeting the criteria post-transformation were discarded to ensure prerequisites for the statistical analysis of ANOVA.
The last step prior to cluster analysis was conducted to reduce dimensionality in the datasets. The reasons for this step were first and foremost interpretability for practical application as well as avoiding a weighting of features representing similar constructs. Dimensionality reduction procedures can be categorized into extraction/construction and selection (Hancer et al., 2020). While the former creates new, often hard-to-interpret features, the latter maintains original features, omitting redundant ones. Prioritizing feature interpretability, we therefore selected the minimum redundancy maximum relevance (MRMR) algorithm (Darbellay & Vajda, 1999; Ding & Peng, 2003; The Mathworks Inc., 2023). Since MRMR requires categorical dependent measures, we segmented real decimal performance into three categories using tertial quantiles, ensuring no score overlap. The number of selected features was determined by consensus of the two authors, considering the ranks of the relevance scores of the MRMR algorithm and interpretability of the features for sports practice.
To choose the appropriate number of clusters, we used the dendrogram as our guiding tool (Backhaus et al., 2021). It offers a visual representation of the clustering process, enabling an intuitive understanding of the relationships and distances between clusters. Meanwhile, the elbow method, a widely recognized technique for identifying the point where the addition of more clusters does not significantly improve the fit of the model, allowed us to quantitatively assess the appropriate number of shot styles for our analysis. This systematic approach ensured that the chosen number of clusters, or shot styles, was not only statistically justified but also meaningful for interpreting differences in shooting performance inter- and intra-individually.
Because we assumed differing numbers of shots per shot styles and therefore different variances for the dependent measure we performed a Welch-ANOVA with post-hoc Games-Howel correction for both datasets. We used the factor shot styles and the dependent measure real shooting performance. Analysis was performed with IBM SPSS Statistics (Version 29) and ω2 was used as an effect size measure (Field, 2013).
Results
Participants
A total of 3973 shots from 53 participants were registered during the measurement period. After data processing 26 out of 53 achieved the minimum required number of shots (50) across different sessions. For a detailed overview on the two datasets consider Table 2.
| HE | SING |
|---|---|---|
N athletes | 26 (77% ♀) | 1 (♀) |
N shots per athlete | 50 | 5,009 |
N shots total | 1,300 | 5,009 |
M ± SD top-3 results of nat. and int. competitions May 2021 – August 2023 | 626.03 ± 3.46 | 632.17 ± 0.76 |
Validation of phase segmentation
In the validation phase of our study, we examined the accuracy of our approach detection algorithm. Out of the initial 720 shots analyzed, one shot had to be excluded due to the algorithm's inability to accurately process an exceptionally brief aiming period. This left us with 719 shots that were suitable for further analysis. To validate the effectiveness of our approach detection algorithm, we compared its performance against the assessments made by three independent shooting experts. The comparison was quantified using Pearson correlation coefficients. The results, detailed in Table 3, reveal significant correlations between the judgments made by the experts and the classifications provided by the approach detection algorithm. These correlations, all statistically significant at p < .05, underline the algorithm's robustness in mimicking expert evaluations of shooting phases.
Data reduction and identifcation of shot styles
After feature calculation, we visually inspected feature histograms to identify any ceiling effects for feature removal. Features tire, aimingAccuracy105, aimingAccuracy10, and hold10a0 exhibiting such effects were subsequently discarded in SING, tire was removed for HE. Single shots were excluded based on hierarchical outlier removal and unsuccessful single shot processing. After the draw of shots for HE, normal distribution checks were conducted. If the feature was not normally distributed, features were Box-Cox transformed to achieve normal distribution. All features of both datasets achieved an absolute skewness value of < 0.5, either with or without Box-Cox transformation (Hatem et al., 2022).
| Expert 1 | Expert 2 | Expert 3 |
|---|---|---|---|
Expert 2 | .79* | - | - |
Expert 3 | .84* | .80* | - |
approach detection algorithm | .84* | .80* | .79* |
df = 717, *p < .05
The MRMR (Darbellay & Vajda, 1999; Ding & Peng, 2003) algorithm then prioritized features based on their relevance and redundancy. After we sorted and plotted the features by scores, we noticed that using an elbow criterion would not make sense, as only one feature would be determined for SING. Based on the operationalization of the feature, the high relevance quickly became clear. It is, in fact, the feature relTimingTargetCentre, which defines the direction of the last trajectory before the shot release. Aiming point movements leading towards the target center are most likely to cause more central hits, while aiming point movements moving away from the center are more likely to cause more distal hits, therefore it is clear that this feature receives the highest relevancy score with regards to shot performance. However, to rely not only on one feature for shot style description, the next three most relevant features were included despite not meeting the elbow criteria, so in total the 4 highest-ranked features were chosen for each dataset separately. For SING the features relTimingTargetCentre, relImpulse, aimMeanVelocity and aimingError were selected and for HE relTimingTargetCentre, aimingAccuracy105, appMeanVelocity and relImpulse were ranked the most relevant. Finally, 5,009 single shots for SING and 1,300 for HE entered the stage for cluster analysis. The dendrograms and the elbow methods for both datasets suggested an optimal solution of four distinct clusters for SING and four for HE. To detail the differences between shooting styles within the two datasets (HE and SING), we refer to Table 4 and Table 5 for a description of the identified clusters. Figure 1 and Figure 2 display the feature distribution of the various shot styles for both datasets based on z-scores.
| Precision hold | Dynamic | Anchored jerk | Erratic jerk |
|---|---|---|---|---|
N shots | 1,288 | 1,070 | 1,398 | 1,253 |
Description | low aiming error, low mean velocity during hold and aiming phase, low displacement of aiming point towards target centre during release phase | high velocity of aiming point during hold and aiming phase | low aiming error, low aiming point velocity during hold and aiming phase, aiming point motion away from target centre | high aiming error, aiming point motion with high displacement during release phase towards target centre |
Performance [radial error in mm] | M = 1.040 SD = 0.588 | M = 1.199 SD = 0.701 | M = 1.464 SD = 0.640 | M = 1.329 SD = 0.735 |
| Sharp deviation | Swift breakaway | Gentle draw-in | Accurate anchor |
|---|---|---|---|---|
N shots | 233 | 235 | 264 | 568 |
N athletes | 26 | 24 | 26 | 26 |
Description | high aiming point displacement during release phase away from target centre | fast approach velocity, high aiming point displacement during release phase | low approach velocity, low aiming accuracy, motion of aiming point towards target centre | high aiming accuracy, low aiming point displacement during release phase |
Performance [radial error in mm] | M = 1.909 SD = .826 | M = 1.652 SD = .846 | M = 1.374 SD = .687 | M = 1.040 SD = .524 |
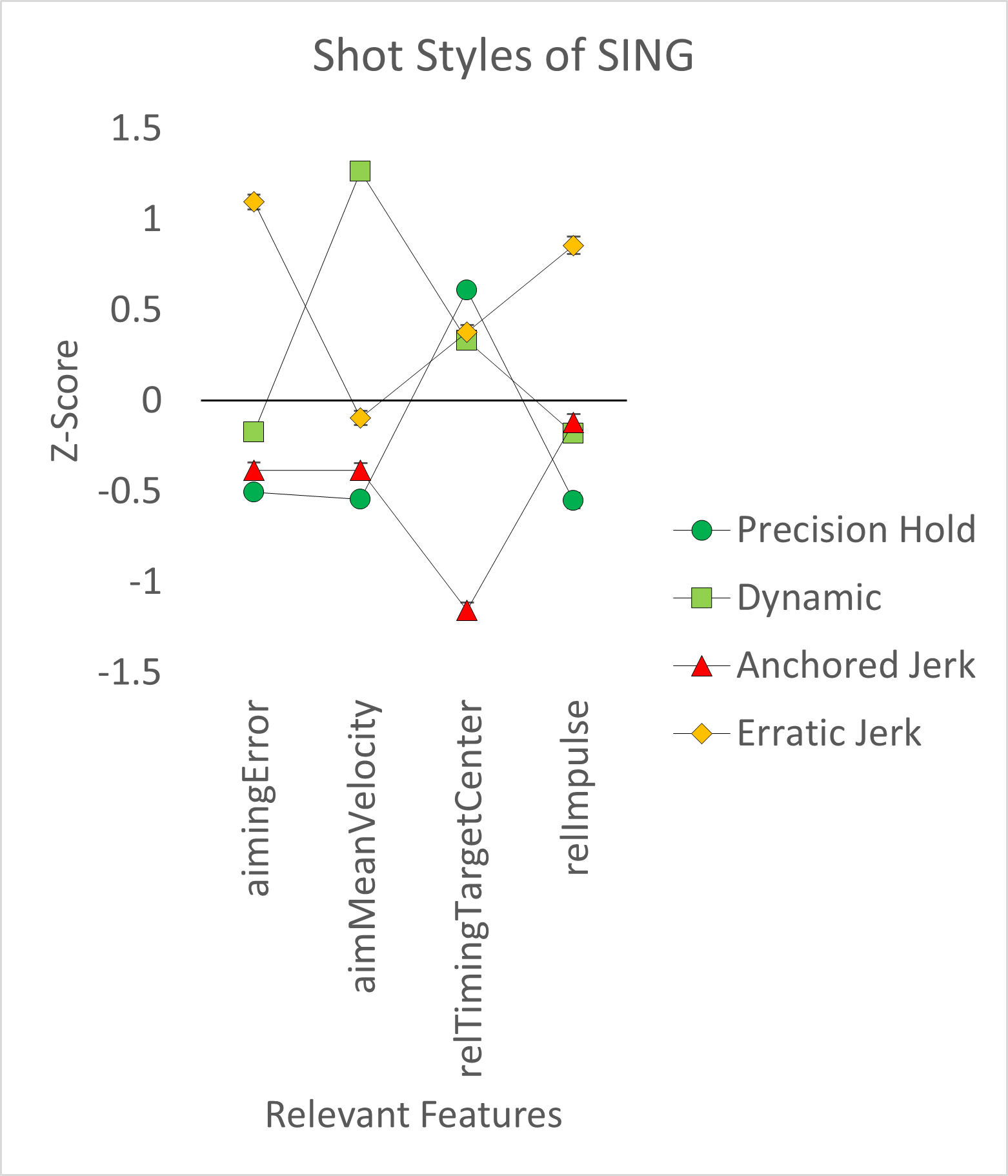
Error bars correspond to 95% confidence interval. The mean decimal real performance scoring for each shot style of SING are as follows: Precision Hold achieved a score of 10.53, Dynamic scored 10.47, Anchored Jerk scored 10.37, and Erratic Jerk scored 10.42.
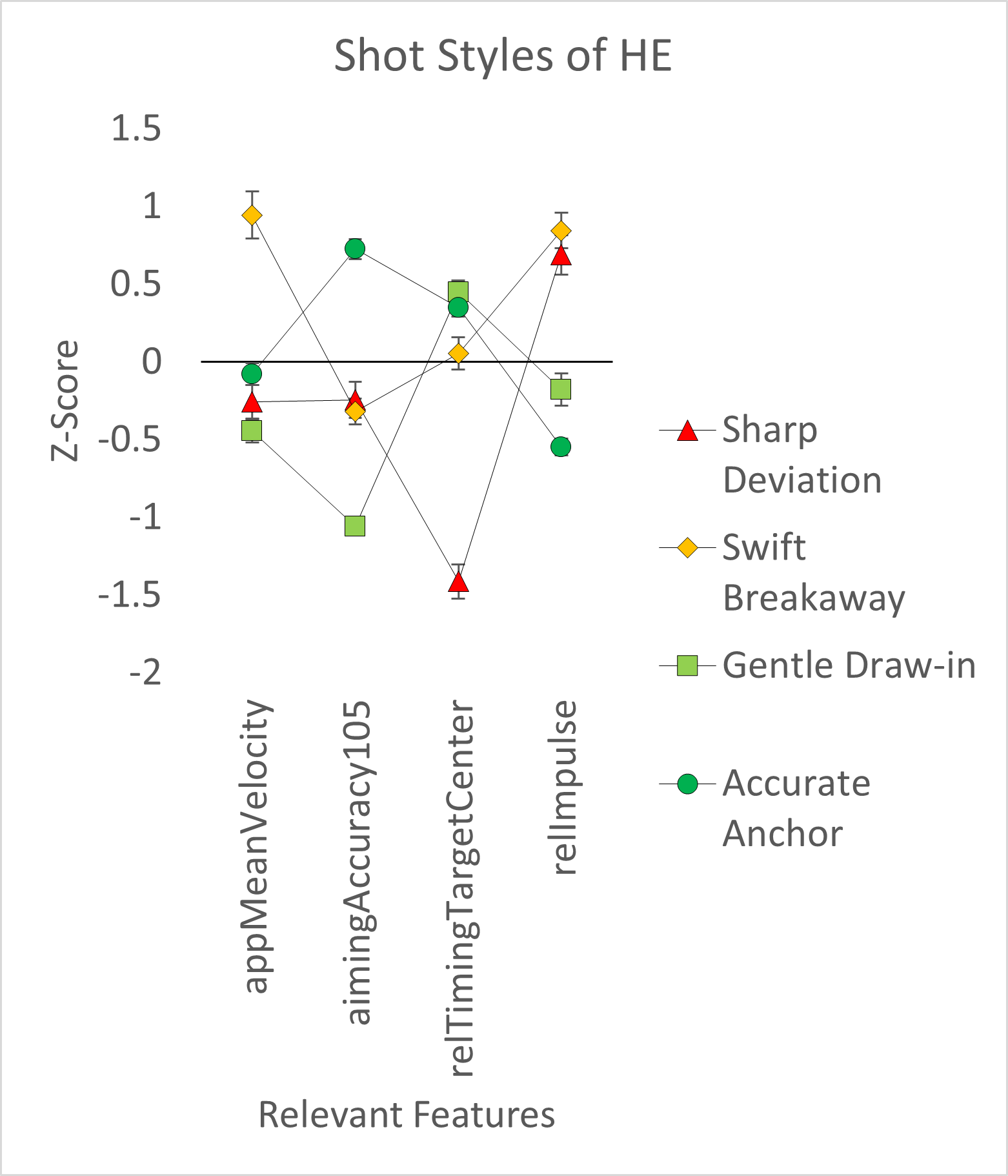
Error bars correspond to 95% confidence interval. The mean decimal real performance scoring for each shot style of HE are as follows: Sharp Deviation achieved a score of 10.18, Swift Breakaway scored 10.29, Gentle Draw-in scored 10.40, and Accurate Anchor scored 10.54.
Performance relevance of shot styles
In our analysis, we applied a Welch one-way ANOVA to assess the impact of four distinct shot styles based on our cluster analysis on real shooting performance, while considering the assumption of homogeneity of variances. For the HE dataset, significant differences were observed among the shot styles, as indicated by the ANOVA (F(3, 510.420) = 100.076, p < .001, ω2 = .186). A subsequent post-hoc Games-Howell test provided a detailed comparison between each pair of shot styles, confirming significant performance discrepancies among them. Specifically, the “Accurate Anchor” style emerged as the most effective, exhibiting the lowest mean radial error (M = 1.040, SD = .524), followed in descending order of performance by “Gentle Draw-In” (M = 1.374, SD = .687), “Swift Breakaway” (M = 1.652, SD = .846), and “Sharp Deviation” being the least effective (M = 1.909, SD = .826).
Similarly, in the SING dataset, the Welch one-way ANOVA revealed significant performance differences across the shot styles (F(3, 2707.825) = 113.326, p < .001, ω2 = .063). The post-hoc Games-Howell test detailed the performance ranking among the styles, with “Precision Hold” being the top performer (M = 1.040, SD = .588). This was followed by “Dynamic” (M = 1.199, SD = .701), “Erratic Jerk” (M = 1.329, SD = .735), and “Anchored Jerk” ranking as the least effective (M = 1.464, SD = .640).
Discussion
Phase segmentation
The validation of our approach detection algorithm revealed a moderate to high mean Pearson correlation (r(717) = .81) between the algorithm-driven phase detection and the classifications made by three independent experts. Intriguingly, the average correlation coefficients among the experts themselves (r(717) = .81) matched those between the experts and the approach detection algorithm. This equivalence underlines the algorithm’s competency in classifying movement phases of the aiming point fluctuations as effectively as human experts, thereby reinforcing its potential applicability in sports shooting research for movement phase segmentation. Notably, the variation in correlation coefficients, ranging from r(58) = .36 to r(58) = .95, highlights the significant inter-athlete differences observed both among the experts and in comparison to the approach detection algorithm. This finding is crucial when considering the optimization of the approach detection algorithm to accommodate diverse shooting styles, as suggested by other researchers (Liu & Mao, 2000; Yli-Jaskari & Heinula, 2009). Further, the challenge of classifying multistage aiming patterns (Zatsiorski & Aktov, 1990) as alternating between stationary phases and directed movements, illustrates potential areas for refinement in our algorithm. While experts tend to identify the last stationary phase before a shot, our approach detector highlights the initial movement that falls below the detection threshold, showcasing a critical area where our method diverges from traditional expert analysis.
Taking a detailed look at the approach techniques employed by elite shooters reveals that broadly applying the term "aiming" to every action from the moment the aiming point enters the target's scoring area doesn't entirely capture the complexity of what occurs. Beyond the visually guided approach to the centre of the target, there may exist a non-visual approach as well. In the latter case, shooters would not rely on visual control to direct their aim; instead, they depend on the natural point of aim to guide the aiming point into alignment.
The natural point of aim is a fundamental concept in precision shooting (Bühlmann & Reinkemeier, 2022; Hariri et al., 2012; Reinkemeier, 2004), emphasizing the importance of aligning the shooter's body and the rifle in a way that naturally aims at the target, minimizing reliance on muscular effort. Since muscular support alone is inadequate for maintaining a stable shooting position across multiple shots, shooters must instead depend on skeletal (non-muscular) support. This approach leverages the more rigid structures of the body to form a stable base, effectively reducing the impact of muscle fatigue and the associated aiming discrepancies over time. Additionally, the reduced reliance on muscle tension helps diminish the involuntary movements or shaking that can detract from shooting accuracy. At the heart of achieving a reliable natural point of aim is the principle of muscular relaxation. A relaxed posture enables the shooter to hold the rifle more steadily, thereby enhancing aiming accuracy. The process requires minimizing muscle tension throughout the body; tense muscles can introduce unnecessary rifle movement, undermining the stability of aim. By focusing on bone rather than muscle to support the weight and balance of the rifle, the shooter can achieve a more consistent aim, shot after shot (Hariri et al., 2012). Ideally, natural point of aim, which varies in accuracy with each shot depending on how precisely the shooter's position is established, aligns perfectly with the center of the target, acting as an attractor gently pulling the aiming point towards the natural point of aim.
Thus, when defining aiming times as starting from the entry of the aiming point into the target's scoring area, this conceptualization of aiming doesn't necessarily apply to all shooters (Ihalainen, Kuitunen, et al., 2016; Janelle et al., 2000). It specifically doesn't apply to those not trained to visually check their approach towards the target but to let themselves be drawn by the natural point of aim without visual confirmation throughout the approach phase. Such differentiation is crucial for understanding the intricate strategies elite shooters employ to optimize their performance.
Identification of shot styles
Through cluster analysis, compensation-sensitive shot styles were identified for both datasets. The features used for the cluster analysis were selected through a feature selection process which does not create new components as principal component analysis (Ball et al., 2003) would, but which evaluates the relevance of individual features in relation to real shooting performance. In contrast to previous works where authors (Ball et al., 2003; Ihalainen et al., 2015; Mon et al., 2019) have used linear models to predict shooting performance, we used cluster analysis to account for compensation mechanisms as stated by other researchers (Arutyunyan et al., 1969; Baca & Kornfeind, 2012; Liu & Mao, 2000; Yli-Jaskari & Heinula, 2009; Zatsiorski & Aktov, 1990).
The features used for clustering were selected from a multitude of potentially relevant features based on an algorithm that evaluated the features in terms of their relevance and redundancy with respect to shooting performance (Darbellay & Vajda, 1999; Ding & Peng, 2003). The features we selected partially correspond to the features identified in a previous work by Ihalainen, Kuitunen, et al. (2016). They could predict 81% of the virtual performance using multiple linear regression through the features stability of hold, cleanness of triggering, aiming accuracy, and timing of triggering. In our study, we had to exclude timing of triggering (tire) due to ceiling effects; however, we introduced a comparable feature, relTimingTargetCentre, which also operationalizes timing, not in terms of time but spatially and directionally, that made it to the top 4 features in both datasets. Cleanness of triggering reached the top 4 features as well with the feature relImpulse, which in turn represents a similar skill associated with triggering the shot. Aiming accuracy made it to the top 4 in HE, and in SING too, aiming accuracy is represented by the feature aimingError. We operationalized stability of hold in various ways, but only one subcomponent (aimMeanVelocity) made it to the top 4 features in SING. Interestingly, a previously unconsidered feature reached the top 4 in HE, namely the variable appMeanVelocity, which represents the approach speed. Another interesting fact is that no variable representing stability of hold made it into the top 4 of HE. This fact is in stark contrast to the statement that stability of hold alone accounts for 54% of the virtual shooting performance (Ihalainen et al., 2015). In general, we achieve similar results in feature selection by applying MRMR as we did with multiple linear regression.
In contrast to previous research, we continued after feature selection and identified shot styles based on combinations of the selected features. This allowed us to identify task solution patterns that vary in real shooting performance. Interestingly, only a subset of all possible selected feature combinations was actually used by the athletes. This indicates that potential task solutions are constrained to certain parameter ranges depending on the current state of the motor system leading to such observable patterns, also termed attractors in research on motor control (Haken et al., 1985; Hossner et al., 2020), and in our case the 4 shot styles identified in both datasets.
Interestingly, such attractors are also described in practical sports shooting literature (Bühlmann & Reinkemeier, 2022), e.g., the concept of the natural point of aim. This concept emphasizes that a shooter should align and correct its neutral skeletal posture before every shot, in such a way that the muzzle points to the centre of the target without any corrective muscular forces applied. A consequence of a non-aligned natural point of aim are sudden aiming point deviations from the intended aiming center during the shot release, ultimately leading to an offset shot location, as present in the identified shot styles Anchored Jerk (SING) and Sharp Deviation (HE), which show only low to medium aiming errors.
Performance relevance of shot styles
The aim of the present study was to identify skill-related mechanisms for performance in Olympic air rifle shooting. Our main results show significant performance differences between shot styles both at the intra-individual level (SING) and inter-individual level (HE). In SING, real performance differences were observed within the four identified shot styles of a single athlete who already exhibited a very high level of performance. Such differences were also present in HE, a more heterogeneous dataset on an inter-individual level comprising multiple athletes of varying skill levels.
Performance differences as minimal as 0.25 mm per shot can distinguish between advancing to the finals or ranking 40th in a World Cup competition. The application of two distinct datasets, which included past participants of the World Championships, underlines that variations in performance due to differing shot styles are not confined to suboptimal performance levels. Notably, within SING, where all shots were executed by a single elite athlete, unique shot styles were identified, each presenting a significant and relevant performance level.
We recognize that by utilizing real performance instead of virtual performance, we might have risked encountering lower effect sizes, as ballistic processes or material properties introduce additional variance, which wouldn’t be present in purely virtual performance. Nevertheless, the results obtained in this study support the continued use of real shooting performance as a performance measure.
Limitations and perspectives
One limitation of our study lies in the hierarchical structure of our datasets. In HE, we encounter a three-tiered structure, encompassing multiple shots across different sessions and athletes, while SING offers a simpler two-tiered structure since all shots are from one individual but from multiple sessions. We compensated this limitation by guaranteeing a representative draw (similar mean and standard deviation) of a minimal number of shots for each athlete within HE. Moreover, while we ensured an equal shot count for each athlete to prevent biased weighting, these shots spanned different sessions, underscoring the need for further investigations into the temporal consistency of shot styles intra-personally and their stability with the inclusion of new shots from different athletes. Lastly, a potential bias in SING emerges from the movement-related feedback given to the athlete during measurements. It is plausible that the athlete’s behaviour adapted based on coaching guidance. This contrasts with HE where movement-specific feedback was intentionally omitted. This disparity in feedback protocols could introduce biases in SING, potentially affecting the discerned shot styles. We tried to compensate for this incongruency in protocols by strictly separating the inter-individual HE dataset from the intra-individual SING dataset at all steps of our analysis.
Regarding research perspectives, several recommendations can be made. First, the proposed approach detector provides a new way to classify aiming point fluctuation into functional movement phases. Second, it is advisable to use real performance as the dependent performance measure instead of virtual performance, preferably including directed position data of shot location. For future research projects in sports shooting, it could be interesting to explore the prediction of directions of real shot position on the target using features derived from aiming point data or other biomechanical data. Third, it is recommended to apply pattern-based methods, as they can better capture compensation effects and allow for a thorough functional understanding of the shooting task. Fourth, a study on the trainability of shot styles could be considered. Shooters may vary their approach behavior, aiming times, and trigger control depending on their daily condition or situational demands. A relevant question for sports practice would be, for example, if shot styles differ under time constraints such as time pressure. Fifth, it is notable that a significant portion of the selected features were from the release phase. This raises the question of how pressure profiles at the trigger coincide with the position of the aiming point fluctuation on the target. Additionally, the influence of rifle characteristics on aiming point features has not been explicitly investigated yet. From biomechanics it is known that more inert objects need more force to identically deviate from a trajectory. Transferring this to the rifle shooting context, an increase in the inertia tensor could be of high practical relevance in terms of predictability and controllability of the aiming point fluctuations. Thus, low involuntary contact forces will not influence rifles with high inertia as much as rifles with low inertia. Lastly, returning to shot styles, it would be valuable to understand the temporal stability of these shot styles. If there is high temporal stability, shot styles could also be used for talent selection aspects especially in countries with larger talent pools.
The implications for practice concern training philosophies and the use of aiming point analysis systems. While using state-of-the-art aiming point analysis systems, coaches should consider compensation aspects and not solely focus on improving individual features. Additionally, the relevant features may vary among individuals. Certain combinations of features may be particularly promising, while others may hinder performance. Individual analyses are necessary to determine the most appropriate feature combinations for each athlete.
Conclusions
Our study revealed that accounting for the interplay among performance relevant features of functionally and empirically divisible movement phases allows us to group shots and identify performance relevant shot styles on both inter- and intraindividual level.